Rivers of Spacetime
Understanding What Gravity Actually Is
One of the main goals of this blog is to convey a deep and useful understanding of how the world works. Few things are more fundamental than gravity and inertia and space and time. And while the everyday applications of this understanding aren’t huge, I find it enlightening and energizing to understand every part of this Universe in which we find ourselves.
When most people try to explain how gravity works according to Einstein’s General Relativity, pretty much every description of how spacetime curves calls upon a particularly horrid analogy — the elastic sheet. “See? Spacetime reacts to mass just like this trampoline does when I put a bowling ball in it!”
And even most science articles show this, or a grid-graph version of it:
These depictions fail to show what spacetime really does in several ways:
What is the sheet or grid deforming into? The 2d sheet or grid is bending into the 3rd dimension. But in General Relativity real spacetime doesn’t deform into some extra dimension. In the presence of mass it gains a curvature within itself.
It “explains” gravity by including an assumption of gravity in the analogy. The large yellow mass above causes a deeper indentation, so the grid becomes steeper over a wider area. Anything that gets near that indentation of course falls in faster because…things fall down into dips? The analogy is meant to explain why spacetime curvature happens, and why that causes a sensation of attraction or pulling. The grid deformation analogy inherently presumes gravity pulling down, which provides no explanatory power at all.
Spacetime is typically shown to be way too flexible. Most viewers of this analogy come away with the impression that spacetime is extremely flexible, easily perturbed and bent greatly by masses like planets and stars. Grid units are stretched by a factor of 2 or 3 by the Sun. This is far from the truth, and gives a quite wrong impression of spacetime. Spacetime is actually incredibly stiff. For instance, it takes the entire mass of the Earth to deform spacetime by only a few hundredths of a percent. That’s around 10^26 kg, which is a lot of energy (E = mc²).
These three factors combine to give people a very distorted view of spacetime and how its curvature generates gravity wells in the presence of mass.
That said, it is a very complicated subject, with math and notation far beyond what most people are willing to trudge through. Even a lot of physicists have trouble fully understanding and visualizing the consequences of the Einstein Equations at the core of General Relativity.
![Asked in 1919 whether it was true that only three people in the world understood the theory of general relativity, [Eddington] allegedly replied:](https://substackcdn.com/image/fetch/f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fbucketeer-e05bbc84-baa3-437e-9518-adb32be77984.s3.amazonaws.com%2Fpublic%2Fimages%2F38681fc8-91d6-4fa5-9a93-10faa5023b0c_850x400.jpeg "Asked in 1919 whether it was true that only three people in the world understood the theory of general relativity, [Eddington] allegedly replied:")
One day recently while I was driving to work, I was thinking about the Equivalence Principle and curved spacetime. The Equivalence Principle basically says that a person experiencing acceleration (speeding up) in empty space will feel pushed back in their chair due to their inertia; and that another person sitting back in a chair (facing up) in a strong gravity field will feel exactly the same force. To the two different observers, the inertial pull felt while accelerating and the pull of sitting still in a gravitation field are the same.
If these two things really are fundamentally equivalent (it’s a basic assumption of General Relativity), then what exactly is happening to the background spacetime in both situations?
One of the most astounding and beautiful things.
Spacetime itself is three static dimensions of space and one flowing dimension of time. If I am just sitting still in the middle of space, I am still flowing forward in time (or moving along with the flow of time). This is a crucial point: the time dimension has a sort of flow to it, even when no energy or movement is involved. We are always moving forward in at least one dimension (time), even when we feel completely still.
Our felt coordinates of flowing time and three dimensions of space are called a Reference Frame. Think of it as how space and time are measured by you. 1 meter east is 1 meter east, and one second of flowing time is 1 second of flowing time. Things get weird at high speeds and high gravity1, but otherwise your reference frame is just how you perceive the world in a normal way.
When you are still, Relativity says you have a reference frame that appears to you to be undistorted. Also, when you are moving at a constant velocity, you still have a reference frame that appears to you to be undistorted. By “undistorted,” I mean that the space directions act fully like space (you can move back and forth in them with nothing weird happening) and time stays fully like time (it flows at one second per second, and only goes that one way at the same ticking speed). And your reference frame is undistorted if you have a constant velocity, whether that velocity is zero or 1 million miles per hour. It’s only when we change velocity, when we accelerate, that our reference frame becomes distorted in a way that generates a force that we can feel.
What kind of distortion is that? Here is an astounding part: when you accelerate (or decelerate) your flowing time dimension is partially converted into a spatial dimension.
Yeah, you’ll want to go back and read that again.
In an accelerating situation, your reference frame as you perceive it is actually distorted such that a little bit of your flow of time is felt by you as a “flow of space,” a tug on you that you feel as inertia. In General Relativity, your reference frame — you — getting accelerated converts a little bit of your flow in time into a feeling of space dragging you backwards from your direction of acceleration.
What is the conversion rate of converting flowing time into space? The answer is the speed of light (300,000,000 meters per second) squared2. Because 300,000,000 m/s 3 times 300,000,000 m/s is a really big number, a tiny bit of flowing time when converted imparts a significant amount of felt inertial force in the space dimension in the opposite direction of your accelerating reference frame.
In the equation below, the triangles (Δ) mean delta, or the amount of change in that thing. The amount of spacetime one traverses (Δs) is the change in x (space) minus c squared times the change in the flow rate of time (Δt), except all factors in the equation are squared. This is what I mean by the conversion rate of space into time. You can see how a small change in t (Δt) would necessitate a pretty significant change in Δx if Δs stays the same value, which it does.
But what about the Equivalence Principle and the pull of gravity we feel while sitting here on a planet? It turns out that gravitational fields actually turn a part of the flow of time into a perceived pull within space. So just like with an accelerating reference frame, the pull you feel is the flow of time getting just a little bit converted into a pull within space.
That is what gravity actually is.
This amazing animation by the YouTube channel ScienceClic illustrates this extremely well. I have linked their excellent 11 minute video on the subject at the end of the article.
That is why accelerating at 9.8 meters/second per second (Earth’s gravitation pull) feels exactly the same as sitting on the surface of earth in a gravitational field with the ability to accelerate objects at 9.8 meters/second per second. Both are basically exchanging the flow of time for the feel of the pull of space in a certain direction. One we call “inertia” and the other we call “gravity.”
They are sort of the same thing, caused by the same conversion of the flow of time into a felt pull in space.
This sounds odd and new, but I am not saying anything new here. This is actually what the math of General Relativity actually says, and this description will match what you hear from almost all respected General Relativity physicists. Matt O’Dowd explains how space and time are exchanged with each other in the strong gravity field of a black hole. Andrew J.S. Hamilton et al wrote a beautiful paper on the subject, noting that his team was far from the first to understand General Relativity this way. The first people to actually realize that gravity is space flowing due to time being converted were actually Allvar Gullstrand4 and Paul Painleve´5 in 1921, just six years after Einstein published his theory. In fact, this flowing-spacetime understanding of General Relativity is actually called the Gullstrand-Painleve´metric. So as weird as this explanation sounds, it really is just a plain language description of what most physicists understand mathematically.
Further, this also helps us more intuitively explain a couple of really weird things about Relativity. The faster we speed up, the slower time goes. That’s because in order to accelerate to that speed, we had to convert our reference frame’s flow of time into space-pull inertia that we had to overcome with a lot of rocket energy (or whatever). Time actually moves slower for a person travelling close to the speed of light. They will actually age less during a fast trip than a stationary person who never accelerated. Because that acceleration exchanged some flow of time for some pull of space (felt as inertia being overcome).
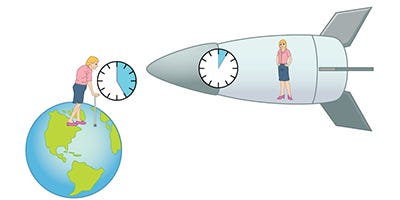
And in gravitational wells, like near planets or stars or black holes, time actually ticks slower versus what would be observed by someone far from the gravity well. This has been measured many times. Atomic clocks at the bottom of a tower tick slower than atomic clocks at the top of a tower. You’ll remember the few hours on the wave planet in Interstellar that meant 14 years to the orbiting spacecraft (a gravitational well that steep they would never have been able to rocket back out of). This happens because the mass of the planet or black hole or whatever is really “bending” the flow of time to convert it into felt spatial pulling. Some time is sort of lost to that pulling. Time flows slower.
Let’s imagine an apple starting out in space 1,000 miles above a planet. As it “feels gravity” and begins to fall, a little bit of its flow of time is converted in a River of Spacetime, along which the apple “wants” to flow. The apple feels at rest. An ant on the apple would feel weightless in its adorable little spacesuit. This is because the reference frame, the space-pulling that the object is embedded in, is in a sense flowing toward the center of the planet, like a River of Spacetime.
Again, I must emphasize the spacetime itself is not flowing and dragging the apple, just like spacetime is not a drag force on an accelerating rocket. But rather, spacetime itself is modified by either a rocket’s acceleration OR the apple’s presence near a strong gravity source (like a planet). And that modification to the local spacetime partially converts an object’s flow of time into a pulling sensation in space that one would feel as either gravity or the inertial force.
This is what gravity actually is: an exchange of the flow of time for a feeling of pulling in space.
I hope you feel this first part is time well-spent. I would only emphasize that this understanding is the standard understanding of how inertia and gravity work. I have not explained anything new. I just sort of got fed up with people explaining General Relativity in a way that glossed over the fact that we exchange time for space when accelerating or sitting in a gravity field. That is just really cool!
And I hope this space article was a good exchange for your time.
=================================================
Author’s Note: If you want to see even more amazing animations on this exact subject, I highly recommend you watch ScienceClic’s 11 minute video:
And technically at high pressures and high electrical charge concentrations…
Really, the speed of Causality squared. Light, the strong force, the weak force, and gravity all propagate in a vacuum at exactly the speed of light, which is really the speed of causality in our universe.
About the speed of light (causality)
Allvar Gullstrand, “Allgemeine L¨osung des statischen Eink¨orperproblems in der Einsteinschen Gravitationstheorie”, Arkiv. Mat. Astron. Fys. 16(8), 1–15 (1922).
Paul Painlev´e, “La m´ecanique classique et la th´eorie de la relativit´e”, C. R. Acad. Sci. (Paris) 173, 677–680 (1921).